Logic Apps (Standard) Data Mapper: Math (or Mathematical) Functions (Part 1)

Overview

Math (or Mathematical) functions are used to perform a variety of mathematical and scientific operations, such as addition and multiplication. If you come from the BizTalk Server background or are migrating BizTalk Server projects, they are the equivalent of Mathematical and Scientific Functoids inside BizTalk Mapper Editor.

Available Functions

The Math functions are:

• Absolute: Returns the absolute value of the specified number.
• Add: Returns the sum from adding two or more numbers.
• Arctangent: Returns the arc tangent of a number.
• Ceiling: Returns the smallest integral value greater than or equal to the specified number.
• Cosine: Returns the cosine for the specified angle.
• Divide: Returns the result from dividing two numbers.
• Exponential: Raises the “e” constant to the specified power and returns the result.
• Exponential (base 10): Returns the number 10 raised to the specified power.
• Floor: Returns the largest integral value less than or equal to the specified number.
• Integer divide: Divides two numbers and returns the integer part from the result.
• Log: Returns the logarithm for the specified number in the specified base.
• Log (base 10): Returns the base 10 logarithm for the specified number.
• Modulo: Returns the remainder from dividing the specified numbers.
• Multiply: Returns the product from multiplying two or more specified numbers.
• Power: Returns the specified number raised to the specified power.
• Round: Rounds a value to the nearest integer or the specified number of fractional digits and returns the result.
• Sine: Returns the sine for the specified angle.
• Square root: Returns the square root for the specified number.
• Subtract: Subtracts the second number from the first number and returns the result.
• Tangent: Returns the tangent for the specified angle.

Absolute

This function states that it will return the absolute value of the specified number.

Behind the scenes, this function is translated to the following XPath function: abs($arg)

• fn:abs($arg as xs:numeric?) as xs:numeric?

Rules:

• If $arg is negative, the function returns -$arg. Otherwise, it returns $arg.
• For the four types xs:float, xs:double, xs:decimal and xs:integer, it is guaranteed that if the type of $arg is an instance of type T then the result will also be an instance of T. The result may also be an instance of a type derived from one of these four by restriction. For example, if $arg is an instance of xs:positiveInteger then the value of $arg may be returned unchanged.
• For xs:float and xs:double arguments, if the argument is positive zero or negative zero, then positive zero is returned. If the argument is positive or negative infinity, positive infinity is returned.

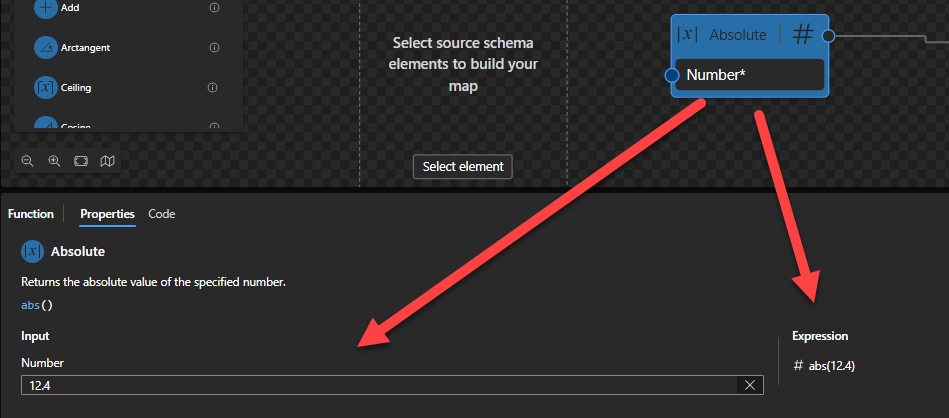
Sample:

• The expression fn:abs(10.5) returns 10.5.
• The expression fn:abs(-10.5) returns 10.5.

Add

This function states that it will return the sum from adding two or more numbers.

Behind the scenes, this function is translated to the following XPath expression: $arg1 + $arg2 (allows more inputs) 

• ($arg1 as xs:numeric + $arg2 as xs:numeric) as xs:numeric

Rules:

• Returns the arithmetic sum of its operands: ($arg1 + $arg2).
• $arg1 and $arg2 are numeric values (xs:float, xs:double, xs:decimal and xs:integer)
• This function allows two or more inputs.

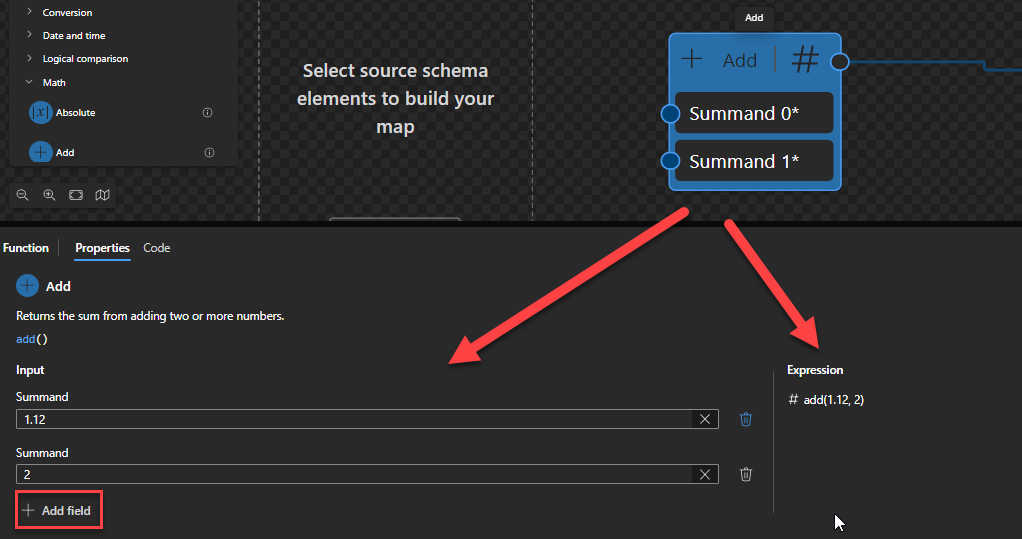
Sample:

• The expression (1) + (3) returns 4.
• The expression (1.12) + (2) returns 3.12.

Arctangent

This function states that it will return the arc tangent of a number.

Behind the scenes, this function is translated to the following XPath function: math:atan($arg)

• math:atan($arg as xs:double?) as xs:double?

Rules:

• If $arg is a non-numeric value, then the result is empty.

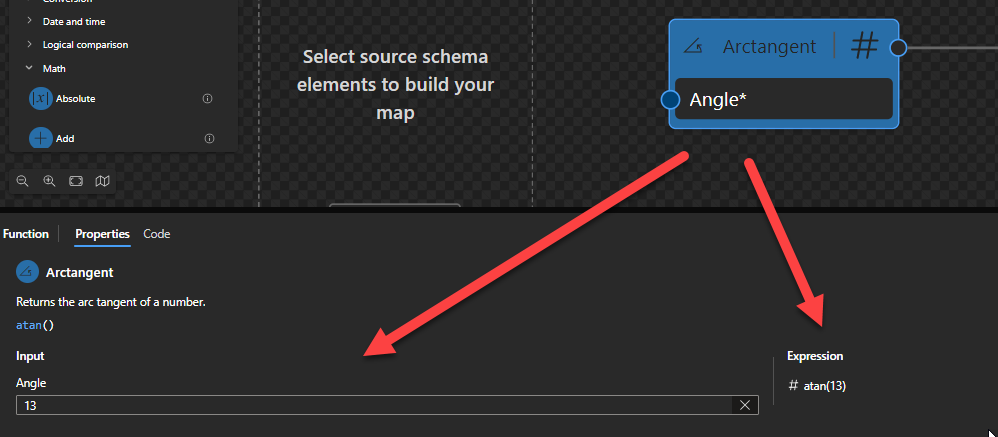
Sample:

• The expression math:atan(0) returns 0.
• The expression math:atan(1.28) returns 0.9075933340888034.

Ceiling

This function states that it will return the smallest integral value greater than or equal to the specified number.

Behind the scenes, this function is translated to the following XPath function: ceiling($arg)

• fn:ceiling($arg as xs:numeric?) as xs:numeric?

Rules:

• The function returns the smallest (closest to negative infinity) number with no fractional part that is not less than the value of $arg.
• For the four types xs:float, xs:double, xs:decimal and xs:integer, it is guaranteed that if the type of $arg is an instance of type T then the result will also be an instance of T. The result may also be an instance of a type derived from one of these four by restriction. For example, if $arg is an instance of xs:decimal then the result may be an instance of xs:integer.

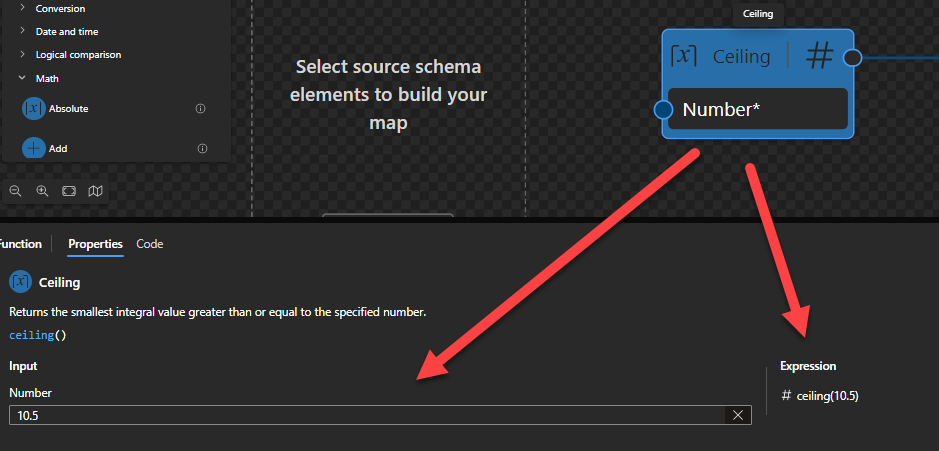
Sample:

• The expression fn:ceiling(10.5) returns 11.
• The expression fn:ceiling(-10.5) returns -10.

Cosine

This function states that it will return the cosine for the specified angle.

Behind the scenes, this function is translated to the following XPath function: math:cos($arg)

• math:cos($arg as xs:double?) as xs:double?

Rules:

• If $arg is positive or negative zero, the result is $arg.

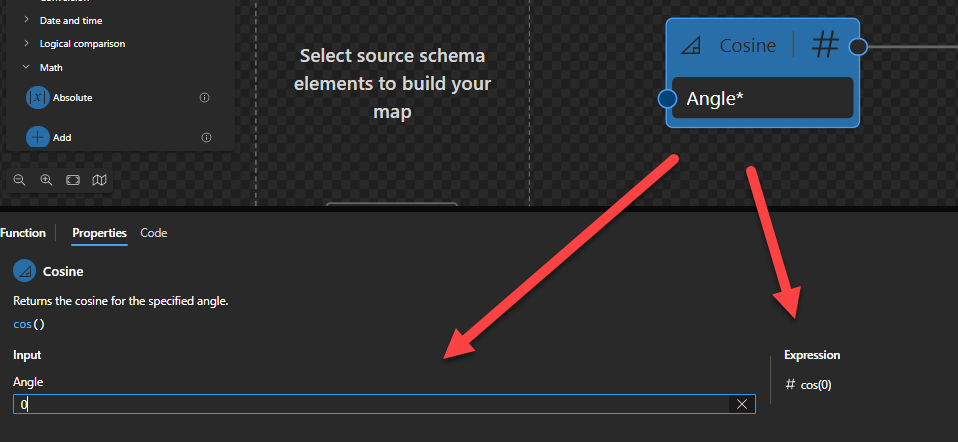
Sample:

• The expression math:cos(0) returns 1
• The expression math:cos(1212) returns 0.7931914936378434

Divide

This function states that it will return the result from dividing two numbers.

Behind the scenes, this function is translated to the following XPath function: $arg1 div $arg2

• $arg1 div $arg2 as xs:numeric?

Rules:

• For the four types xs:float, xs:double, xs:decimal and xs:integer, it is guaranteed that if the type of $arg is an instance of type T then the result will also be an instance of T. The result may also be an instance of a type derived from one of these four by restriction. For example, if $arg is an instance of xs:decimal then the result may be an instance of xs:integer.

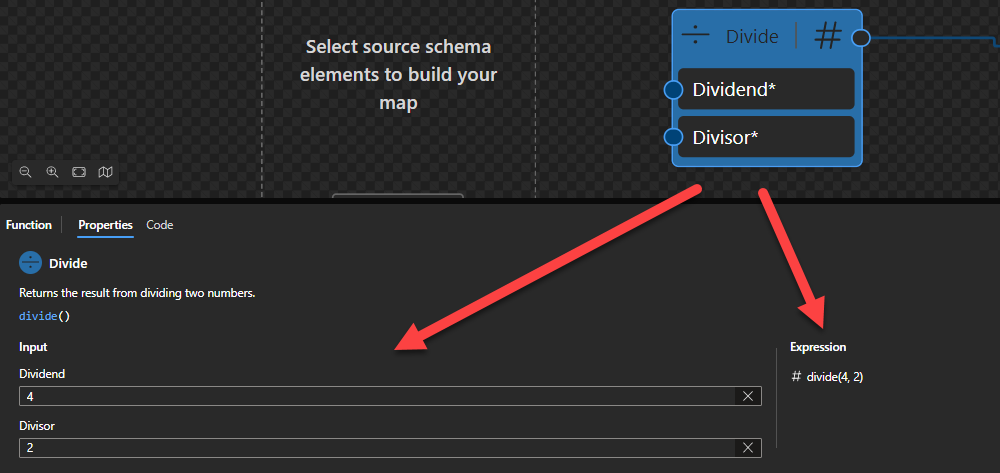
Sample:

• The expression (10) div (3) returns 3.
• The expression (-3) div (-2) returns 1.5.
• The expression (-3) div (2) returns -1.
• The expression (-3.5) div (3) returns 0.7.

Exponential

This function states that it will raise the “e” constant to the specified power and returns the result.

Behind the scenes, this function is translated to the following XPath function: math:exp($arg)

• math:exp($arg as xs:double?) as xs:double?

Rules:

• Returns the value of e

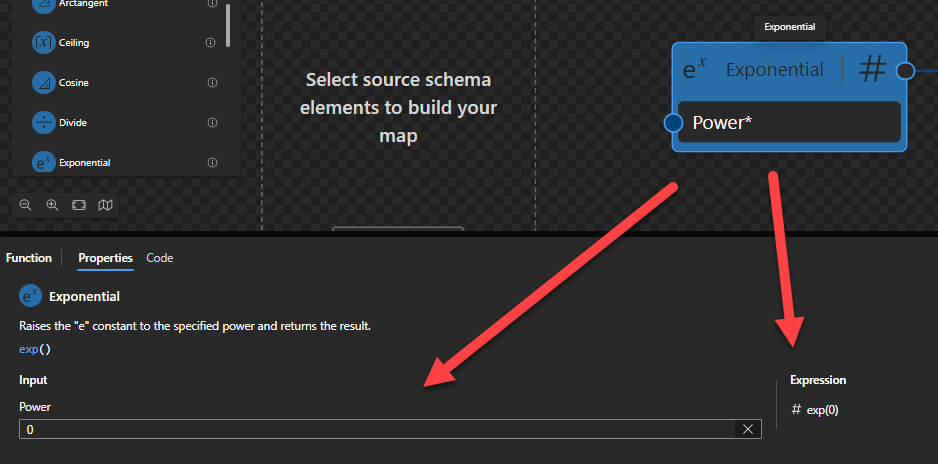
Sample:

• The expression math:exp(0) returns 1.
• The expression math:exp(1) returns 2.7182818284590455.

Exponential (base 10)

This function states that it will return the number 10 raised to the specified power.

Behind the scenes, this function is translated to the following XPath function: math:exp10($arg)

• math:exp10($arg as xs:double?) as xs:double?

Rules:

• Returns the value of 10

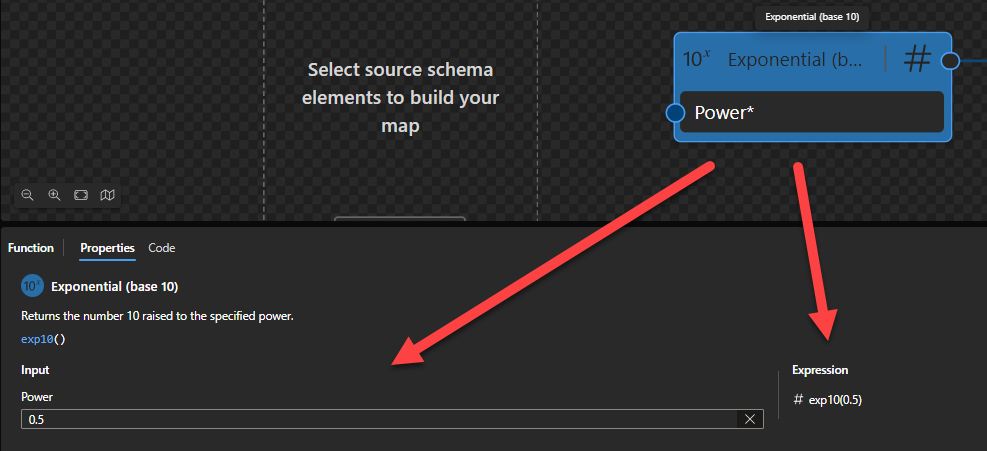
Sample:

• The expression math:exp10(0) returns 1
• The expression math:exp10(1) returns 1.0e1.
• The expression math:exp10(0.5) returns 3.1622776601683795

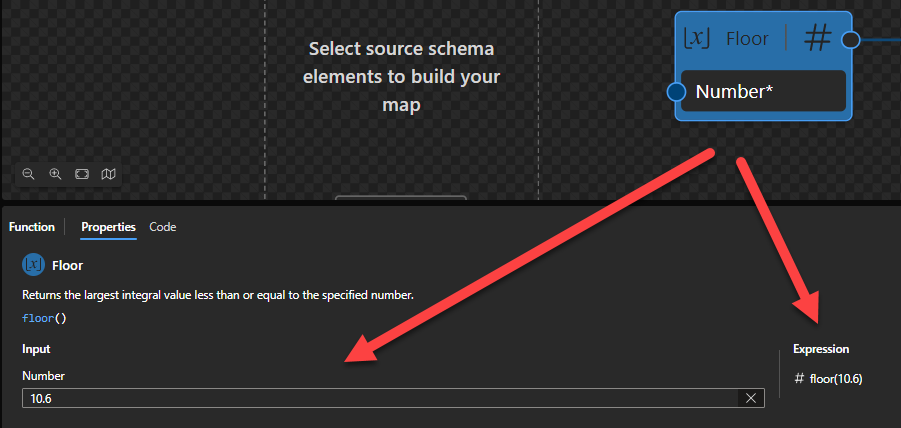
Floor

This function states that it will return the largest integral value less than or equal to the specified number.

Behind the scenes, this function is translated to the following XPath function: floor($arg)

• fn:error($code as xs:QName?, $description as xs:string) as none

Rules:

• The function returns the largest (closest to positive infinity) number with no fractional part that is not greater than the value of $arg.
• For the four types xs:float, xs:double, xs:decimal and xs:integer, it is guaranteed that if the type of $arg is an instance of type T then the result will also be an instance of T. The result may also be an instance of a type derived from one of these four by restriction. For example, if $arg is an instance of xs:decimal then the result may be an instance of xs:integer.

Sample:

• The expression fn:floor(10.5) returns 10.
• The expression fn:floor(10.9) returns 10.
• The expression fn:floor(-10.5) returns -11.

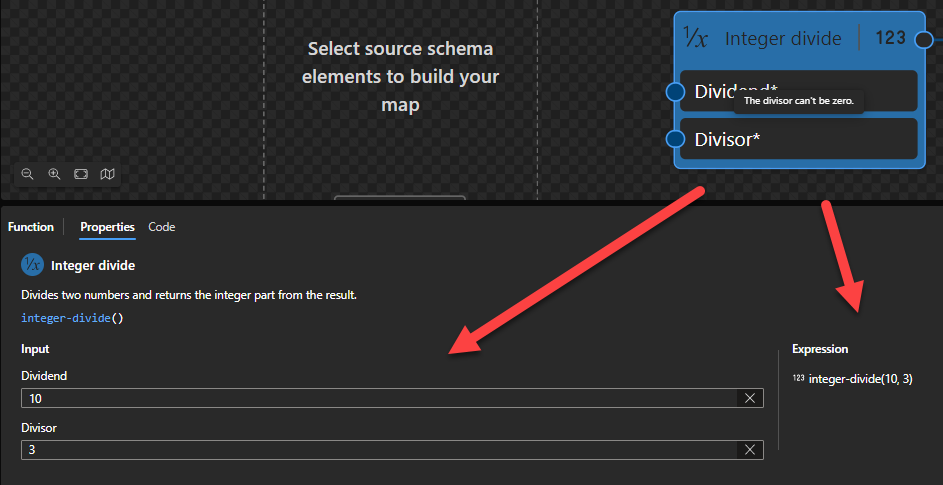
Integer divide

This function states that it will divide two numbers and returns the integer part from the result.

Behind the scenes, this function is translated to the following XPath expression: ($arg1) idiv ($arg2)

• ($arg1) idiv ($arg2) as xs:integer

Rules:

• Performs an integer division.
• For the four types xs:float, xs:double, xs:decimal and xs:integer, it is guaranteed that if the type of $arg is an instance of type T then the result will also be an instance of T. The result may also be an instance of a type derived from one of these four by restriction. For example, if $arg is an instance of xs:decimal then the result may be an instance of xs:integer.

Sample:

• The expression (10) idiv (3) returns 3.
• The expression (-3) idiv (-2) returns 1.
• The expression (-3) idiv (2) returns -1.
• The expression (-3.5) idiv (3) returns -1.

Stay tune for the second part of this blog post.

Hope you find this helpful! So, if you liked the content or found it useful and want to help me write more, you can buy (or help buy) my son a Star Wars Lego!